3. Movimientos en el plano

Un movimiento  o isometría es una transformación en el que todas las figuras mantienen su forma y su tamaño. La distancia entre dos puntos cualesquiera se mantiene constante.

3.1 Las translaciones. ¿Qué es un vector?

Un vector es un segmento orientado. Que además posee:

Origen

O también denominado Punto de aplicación. Es el punto exacto sobre el que actúa el vector.

Módulo

Es la longitud o tamaño del vector. Para hallarla es preciso conocer el origen y el extremo del vector, pues para saber cuál es el módulo del vector, debemos medir desde su origen hasta su extremo.

Dirección

Viene dada por la orientación en el espacio de la recta que lo contiene.

Sentido

Se indica mediante una punta de flecha situada en el extremo del vector, indicando hacia qué lado de la línea de acción se dirige el vector.

3.2 Ejercicios de vectores y translación

3.2.1 Dados los vectores u=(4,3) y v=(-1,4), hallar:

a) su representación gráfica en un sistema de coordenadas

b) los vectores u + v y u - v por la regla del paralelogramo

c) las componentes de los vectores anteriores

d) el módulo de cada uno de los vectores

3.2.2 Dibuja las figuras trasladadas de las siguientes en una traslación de vector guía u(4,3):

3.3 Giros

3.3.1 Ejercicio: Escribe la inicial de tu nombre y haz varios giros con ella.

3.4 Simetría. Ejercicios

3.4.1 Dado el triángulo de vértices A(-2,2), B(6,-1) y C(7,5) se pide:

a) dibujar el triángulo

b) hallar el triángulo simétrico respecto del centro de simetría O(0,0)

c) hallar el triángulo simétrico respecto del eje OX

3.4.2 Euclides (aproximadamente 300 a. C.) enunció las leyes de reflexión de la luz sobre un espejo plano.

Herón de Alejandría, 400 años después, afirmó algo más sencillo: "La luz ha de tomar siempre el camino más corto". Sirviéndote de esta idea, halla en que punto del espejo se ha de reflejar un rayo de luz que parte del punto A para que después llegue a B.

3.4.3 Carlos y Fernando están jugando al billar.

En un determinado momento las bolas se encuentran
en las posiciones indicadas por el dibujo. Indica el camino que debe seguir la bola A para que
rebotando en la banda MQ golpee a la bola B.

Indica el camino que debe seguir la bola A para que rebotando en la banda NP y PQ golpee a la bola B.

3.4.4 Inventa un abecedario simétrico y escribe una frase.

3.5 Frisos, mosaicos y cenefas

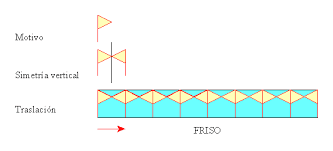
3.5.1 ¿Qué son los Frisos?

En matemáticas, un friso es el cubrimiento de la región del espacio de longitud infinita pero de anchura finita, limitada por dos rectas paralelas^{[ ]}obtenido a partir de la aplicación de movimientos en el plano a una determinada figura o agrupación de figuras.
La combinación de los movimientos de traslación, reflexión, y rotación permiten obtener siete subgrupos de frisos diferentes.

3.5.2 ¿Qué es un Mosaico?

Se llama mosaico a todo recubrimiento del plano mediante piezas llamadas teselas que no pueden superponerse, ni pueden dejar huecos sin recubrir y en el que los ángulos que concurren en un vértice deben de sumar 360 grados. Existen muchas formas de obtener un mosaico, los más sencillos están formados por un único tipo de polígono regular, como el triángulo equilátero, el cuadrado o el hexágono regular.

3.5.3 ¿Qué son las cenefas?

 Una cenefa es un elemento decorativo largo y estrecho que se coloca en una pared rodeando su perímetro o como marco de otros elementos decorativos.

3.6 MC. Escher

Maurits Cornelis Escher (1898-1972). más conocido por sus iniciales como M.C. Escher, es uno de los más grandes artistas gráficos del siglo XX. Tal vez la mejor definición que se ha dado de él sea la de «uno de los más reconocibles y admirados por el gran público». Esto viene a decir que muchas personas admiran y encuentran curiosos, intrigantes y bonitos sus trabajos, aunque al principio no sepan muy bien de quién son ni conozcan realmente al autor o la época en que fueron creados.

Sus más populares obras, figuras imposibles, fondos reticulados con diversos patrones y mundos imaginarios han sido reproducidas hasta la saciedad en portadas de libros, revistas, campañas publicitarias y en todo tipo de formatos. Escher es, en cierto modo, uno de los artistas más referenciados en la «cultura popular» del siglo XX.

Dado que sus obras guardan ciertas similitudes entre sí debido a la recurrencia de los temas tratados (las figuras imposibles, las metamorfosis) son fácilmente «reconocibles» para el observador interesado, que a veces acaba descubriendo al artista tras haberse encontrado previamente con gran parte de su obra.

Tal vez el carácter matemático de sus obras ha hecho también que sea uno de los artistas más populares en los entornos científicos, especialmente matemáticos e informáticos. Curiosamente, sus conocimientos matemáticos siempre fueron muy limitados. Muchas de las conclusiones gráficas y matemáticas a las que llegó, que le permitirían realizar algunos de sus trabajos, tuvo que descubrirlas por sí mismo.

Mini-biografía de M.C. Escher

Maurits Cornelis Escher nació el 17 de junio de 1898 en Leenwarden (Países Bajos), hijo de un ingeniero hidráulico. Era un pésimo estudiante que tuvo que repetir curso dos veces. Para él la escuela era una pesadilla, excepto las clases de dibujo. Como tantos otros grandes artistas, era zurdo. Su profesor F.W. van der Haagen le enseñó la técnica de los grabados en linóleo y fue una gran influencia para el joven Escher.

En 1919 comenzó a estudiar en la Escuela de Arquitectura, pero abandonó sus estudios. A cambio, comenzó a aprender la técnica del grabado en madera o xilografía de Samuel Jesserun de Mesquita, su maestro, que utilizaría posteriormente en muchas de sus obras.

Hacia 1922 fue a Italia de vacaciones y teminaría viviendo en Roma una larga temporada. Le gustaban el clima y los paisajes italianos, y a menudo los recorría a pie en larguísimas excursiones. En 1924 conoció en uno de esos viajes a Jetta Umiker, que se convertiría en su mujer y con quien tendría tres hijos. Muchas de las obras de Escher en las que se ven casas y edificios en la costa están inspiaradas en la arquitectura tradicional de pequeños pueblecitos italianos.

Escher también viajó a España, donde descubriría la Alhambra de Granada, el Generalife y la Mezquita de Córdoba, cuyas maravillas estudiaría con detalle. Lo que aprendió allí tendría fuertes influencias en muchos de sus trabajos, especialmente en los relacionados con la partición regular del plano y el uso de patrones que rellenan el espacio sin dejar ningún hueco.

A partir de 1935, Escher dejó italia entre otras cosas debido al desagradable clima político que se avecinaba y que desembocaría en la II Guerra Mundial, y pasó algunos años en Suiza, cuyo clima le resultó muy desagradable y poco inspirador. Luego fue a vivir a Bélgica en 1937 y finalmente regresó a Baarn, Holanda, en 1941.

Hasta 1951 vivió básicamente dependiendo económicamente de sus padres. A partir de entonces fue cuando comenzó a vender sus grabados y obtener un buen dinero por ellos. Esto le permitió vivir sus últimos años con una economía personal excelente. Generalmente hacía copias de las litografías y grabados por encargo. También hizo por encargo diseños de sellos, portadas de libros, y algunas esculturas en marfil y madera. En cierto modo le resulta gratificante y a la vez fácil, y se admiraba de tener en su taller una especie de «máquina de fabricar billetes» reproduciendo sus propias obras. Normalmente no usaba elementos de obras anteriores en las nuevas nuevas, excepto en los encargos especiales. Hacía, por ejemplo, esculturas en madera basadas en algunos de sus dibujos, y para algunas peticiones especiales reciclaba parte de las ideas y elementos de obras anteriores.

Hasta 1962 su producción de trabajos fue muy constante. Entonces cayó enfermo y eso supuso un pequeño parón transitorio. En 1969 realizó su último trabajo original, Serpientes, que demostraba que su habilidad seguía intacta. Hacia 1970 ingresó en una residencia para artistas en Holanda, donde pudo mantener su propio taller.

Falleció el 27 de marzo de 1972.

A lo largo de su carrera realizó más de 400 litografías y grabados en madera, y también unos 2.000 dibujos y borradores. De muchos existen decenas de reproducciones, cientos e incluso miles de otros. Al final de su carrera destruyó algunas de las planchas para que no se realizaran más reproducciones de originales. También existen estudios y borradores de muchas de sus obras, en ocasiones también varias versiones de algunas de ellas. Muchas de su obras se vendieron masivamente poco después de su muerte y están esparcidas por el mundo. Un grupo importante está expuesto de forma permanente en el Museo Escher en La Haya, Holanda.